Varianssi on mitta, jolla voidaan kuvata, kuinka paljon yksittäiset arvot voivat vaihdella toisistaan otoksessa tai populaatiossa.
Laskemalla varianssin voit tutkia populaation tilastollista käyttäytymistä ja havaita arvojen ja todennäköisyyksien merkityksen kyseisissä numeroissa tai otosryhmässä.
Varianssin laskemisessa on noudatettava sääntöä, jonka mukaan otoksesta tai koko populaatiosta satunnaisesti otettujen tietojen tulee olla tyypillisiä tai toisiinsa liittyviä arvoja, eli ne ovat lähellä keskiarvoa ja toisiaan. Jos mukana on poikkeavia tai huomattavan suuria arvoja, jotka ovat harvassa, ne eivät edusta populaatiota, eikä niitä siksi pidä ottaa huomioon.
Otosvarianssin laskeminen
Otoksen varianssi eli otosvarianssi vastaa laskettua arvoa, joka saadaan kaikkien otoksen arvojen (Xᵢ) summasta vähentämällä keskiarvon (x̅) arvo, jaettuna arvojen lukumäärällä miinus yksi (n-1).
Yksi vähennetään, jotta otoksen arvo suhteessa populaatioon näkyy.
Oletetaan, että taulukosta saadaan seuraavat arvot:
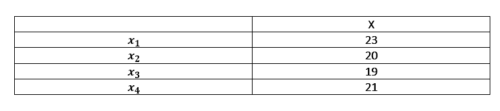
Käytetään seuraavaa otosvarianssikaavaa:
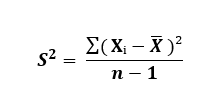
Keskiarvon (x̅) saamiseksi kaikki X-arvot summataan ja jaetaan otettujen arvojen lukumäärällä.
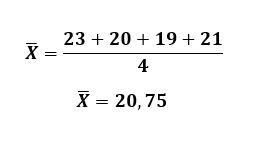
Kun keskiarvo x̅ on laskettu, korvataan summien arvot kaavassa.

Otoksen keskihajonta
Otoksen keskihajonta ilmaistaan samalla yksiköllä kuin varianssi toiseen korotettuna arvona.
Otoksen keskihajonnan määrittämiseksi riittää, että otetaan neliöjuuri exponentin poistamiseksi.
Tässä tapauksessa keskihajonta esitetään merkinnällä (s), ja arvoa ei koroteta toiseen.
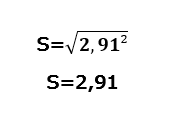
Populaatiovarianssin laskeminen
Populaatiovarianssi kuvaa koko populaation tutkimista, eli otat kaikki arvot määrittääksesi varianssin.
Oletetaan, että edellisen taulukon arvot vastaavat koko populaatiota, ja esimerkki perustuu samaan arvotaulukkoon.

Kaava perustuu samaan periaatteeseen, jossa summataan kaikki populaation elementtien (Xᵢ) arvot vähentämällä keskiarvon (µ) arvo ja korottamalla ne toiseen.
Käyttämällä tätä tulos jaetaan populaatiosta otettujen tietojen lukumäärällä (n).
Tässä käytetään populaatiovarianssin laskentakaavaa σ²:
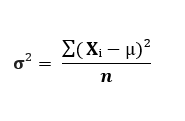
Laskettaessa arvo (µ), lasketaan kaikkien otettujen tietojen keskiarvo. Tässä tapauksessa kaikki X-arvot summataan ja ne jaetaan n:llä, joka on otettujen tietojen lukumäärä.
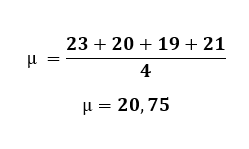
Kun keskiarvo on saatu, tarvitset kaavan arvojen korvaamisen peräkkäisissä vähennyksissä ja summissa.

